
You can use a height and base or you can use d1 times d2 divided by 2. So you've got a couple of options when you're trying to calculate the area of a rhombus.
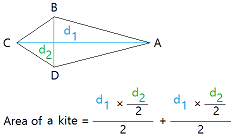
In other words, the area of a kite can be. This figure is called a quadrilateral, in which two pairs of adjacent sides are equal, and which has 4 (four) sides, 4 (four) vertices, and 4 (four) angles. So, this formula of d1 times d2 divided by 2 has to apply. The area of a kite is based on the design of a kite which is a shape with four non-collinear joined points, giving a closed figure with four sides. The other way, is to say well, the diagonals of a rhombus are also perpendicular and they bisect each other. The first way is to say if you know a height and a corresponding base, then you can just calculate the area as base times height. So there's going to be 2 ways for you to calculate the area of a rhombus. The key thing to realizing this formula, was cutting out these pieces, rotating and translating and saying that the diagonals of a kite, that this diagonal is bisected by the other diagonal. Kite Calculator kite Area of Kite Diagonal Method: ×d1d2 kite Area of Kite Using Trigonometry: ab Sin C kite Perimeter of Kite:2(a+b) Related. So another way of writing this is to realise that d2 and d1 are in your numerator, so you just rearrange it and write it as d2 times d1 divided by 2. So the area of this rectangle, our base is d2 divided by 2 times our height which is d1.
#Area of kite how to#
It has 2 diagonals that intersect each other at. Examples, solutions, videos, worksheets, games, and activities to help Geometry students learn how to find the area of kites and. It can be viewed as a pair of congruent triangles with a common base. The two angles are equal where the unequal sides meet. So now we've created since we know that these are all right angles, we have created a rectangle, and we know that the area of a rectangle is the base times the corresponding height. A kite is a quadrilateral that has 2 pairs of equal-length sides and these sides are adjacent to each other. Which means this piece right here is going to be d2 divided in half. This information should be given, or you should be able to measure. Plug the length of the sides into the formula. Want to find the area of a trapezoid If you have the length of each base and the height, you can use them to find the area. This formula works if you are given two non-congruent side lengths and the. Set up the formula for the area of a kite. What else do we know about the diagonals of a kite? Well, I know that this d2 is bisected by the other diagonal. Using an Angle and Two Sides to Find the Area 1. So let's start off by saying well, what do we know? We know that this distance right here is the distance of diagonal 1. So now we have this other piece here that we cut out and up here we have another piece that we cut out. But then I said I translate it and rotate it. So I'm going to redraw my kite, where we have our initial piece which is right here and we have this bottom piece right here. So I'm going to do the same thing with this piece right here.


I'm going to do the the same thing with this piece except and actually by translate I meant translate and then rotate. So what I'm going to do is I'm going to cut out this piece right here out of the white board and I'm going to translate it until it fits into this area right here.

We know that the diagonals in the kite are perpendicular. To find the diagonals, I used the pythagorean theorem for the diagonal that forms the hypotenuse of the. So is there any way that we can take this kite and rearrange its pieces to make a rectangle. To find the area, I used the formula for a kite. We know this area is going to be equal to its base times its corresponding height. We know that the area of a rectangle, so if I write in some right angles, label these as parallel. in an engaging manner by visiting our site BYJU’S.What is the area of a kite where all you know is the length of each of those diagonals? Well, let's go back to what we do know. Learn various related concepts of topics like Quadrilateral, Trapezoid, Rhombus, Rectangle, Square, etc. Unlike a square, none of the interior angles of a rhombus is not \(90^\) Rhombus- A rhombus is a quadrilateral in which all the four sides are of equal length.


 0 kommentar(er)
0 kommentar(er)
